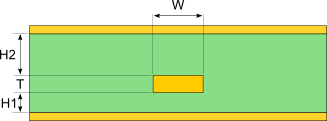
Eine Stripline besteht aus einem flachen Leiter, der zwischen zwei Masseebenen aufgehängt ist. Der Leiter und die Masseebenen sind durch ein Dielektrikum getrennt. Der Abstand zwischen dem Leiter und den Ebenen ist nicht für beide Bezugsebenen gleich. Diese Struktur wird höchstwahrscheinlich mit dem Leiterplattenprozess hergestellt
Ein Beispiel für eine asymmetrische Stripline ist eine 4-Lagen-Leiterplatte, bei der eine Spur auf Ebene 3 sowohl auf Ebene 1 als auch auf Ebene 4 bezogen ist. Die Spur ist der Ebene 4 am nächsten, und die Ebene 4 hat den dominanten Einfluss auf die Impedanz der Übertragungsleitung, aber die Ebene 1 würde die charakteristische Impedanz dieser Spur immer noch beeinflussen.
Die Impedanz Z
0,AS für eine asymmetrische Stripline kann gemäß den Formeln im Dokument IPC-2141A berechnet werden, insbesondere im Abschnitt 4.2.5. Die charakteristische Impedanz wird durch folgende Formel gegeben:
![Z_{0,AS}=\frac{1}{\sqrt{\varepsilon_r}}\left [ Z_{0,SS}(\varepsilon_r=1, b=h_1+h_2+t)-\Delta Z_{0,air} \right ]](https://obrazki.elektroda.pl/7599043000_1718711670.webp) Eq. 1
Eq. 1
wobei:
Z0,SS ist die Impedanz der symmetrischen Stripline, die gemäß Gleichung 1 oder Gleichung 3 des Symmetric Stripline Impedance-Tools berechnet wird und die folgenden Eingabewerte liefert: Ɛr=1, b=h1+h2+t. Z0,SS ist die Impedanz mit Luft als Dielektrikum und einer Gesamtdicke, b, die gleich h1+h2+t ist.
ΔZ0,air wird durch die folgende Gleichung gegeben:
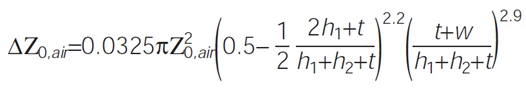 Eq. 2
Eq. 2
wobei h1 der Abstand zwischen der Signalleitung und der unteren Bezugsebene ist, h2 der Abstand zwischen der Signalleitung und der oberen Bezugsebene ist und Z0,air durch folgendes gegeben ist:
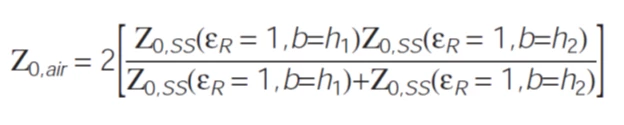 Eq. 3
Eq. 3
Z0,SS ist die Impedanz der symmetrischen Stripline, die gemäß Gleichung 1 oder Gleichung 3 des Symmetric Stripline Impedance-Tools berechnet wird und die wiederum die folgenden Eingabewerte liefert:
- Ɛr=1, b=h1. Es ist die Impedanz mit Luft als Dielektrikum und einer Gesamtdicke, b, die gleich h1 ist
- Ɛr=1, b=h2. Es ist die Impedanz mit Luft als Dielektrikum und einer Gesamtdicke, b, die gleich h2 ist


![Z_{0,AS}=\frac{1}{\sqrt{\varepsilon_r}}\left [ Z_{0,SS}(\varepsilon_r=1, b=h_1+h_2+t)-\Delta Z_{0,air} \right ]](https://obrazki.elektroda.pl/7599043000_1718711670.webp) Eq. 1
Eq. 1
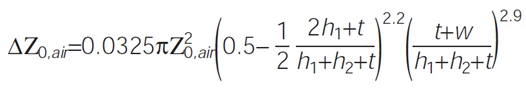 Eq. 2
Eq. 2
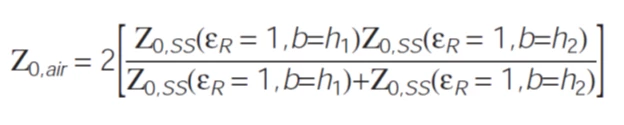 Eq. 3
Eq. 3








