

Czy wolisz polską wersję strony elektroda?
Nie, dziękuję Przekieruj mnie tam
Arithmetische Operationen
Arithmetische Eigenschaften
Beispiele für Operationen
Eigenschaften von Exponenten
Eigenschaften von Wurzeln
Eigenschaften von Ungleichungen
Eigenschaften von Absolutwerten
Komplexe Zahlen
Def. von komplexen Zahlen
Eigenschaften von komplexen Zahlen
Def. von Logarithmen
Logarithmuseigenschaften
Polynome
Quadratische Gleichung
Häufige Beispiele für Faktorisierung
Quadratwurzel
Absoluter Wert
Quadrat vervollständigen
Konstante Funktion
Linear Funktion
Parabel
Kreis
Ellipse
Hyperbel
Die grundlegenden Rechenoperationen sind Addition, Subtraktion, Multiplikation und Division. Diese Operatoren folgen einer Operationsreihenfolge.
Addition ist die Operation, bei der zwei Zahlen kombiniert werden. Wenn mehr als zwei Zahlen addiert werden, nennt man das Summieren. Addition wird durch das Symbol + gekennzeichnet. Die Addition von Null zu einer beliebigen Zahl ergibt dieselbe Zahl. Die Addition einer negativen Zahl entspricht der Subtraktion des Absolutwerts dieser Zahl.
Subtraktion ist die Umkehrung der Addition. Der Subtraktionsoperator reduziert den ersten Operanden (Minuend) um den zweiten Operanden (Subtrahend). Subtraktion wird durch das Symbol - gekennzeichnet.
Multiplikation ist das Produkt zweier Zahlen und kann als eine Reihe wiederholter Additionen betrachtet werden. Die Multiplikation einer negativen Zahl ergibt den Kehrwert der Zahl. Die Multiplikation von Null ergibt immer Null. Die Multiplikation von Eins ergibt immer dieselbe Zahl.
Division ist die Methode zur Ermittlung des Quotienten zweier Zahlen. Division ist das Gegenteil von Multiplikation. Division ist der Dividend geteilt durch den Divisor.
Die wichtigsten arithmetischen Eigenschaften sind Assoziativ, Kommutativ und Distributiv. Diese Eigenschaften werden verwendet, um Ausdrücke zu manipulieren und äquivalente Ausdrücke in einer neuen Form zu erstellen.
Die Assoziativ-Eigenschaft bezieht sich auf Gruppierungsregeln. Diese Regel ermöglicht es, die Reihenfolge von Additions- oder Multiplikationsoperationen mit Zahlen zu ändern und trotzdem denselben Wert zu erhalten.

Die Kommutativität bezieht sich auf die Reihenfolge der Operationen. Diese Regel gilt sowohl für Addition als auch Subtraktion und ermöglicht es den Operanden, innerhalb derselben Gruppe die Reihenfolge zu ändern.

Das Gesetz der Verteilung ermöglicht es in einigen Fällen, Operationen in Teile zu zerlegen. Die Eigenschaft wird angewendet, wenn eine Multiplikation auf eine Divisionsgruppe angewendet wird. Dieses Gesetz wird im Fall der Faktorisierung angewendet.



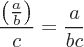
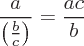

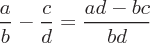

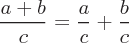
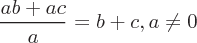



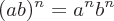


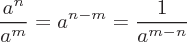

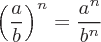



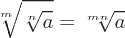

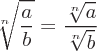







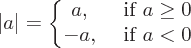





Komplexe Zahlen sind eine Erweiterung des reellen Zahlensystems. Komplexe Zahlen werden als zweidimensionaler Vektor definiert, der eine reelle Zahl und eine imaginäre Zahl enthält. Die imaginäre Einheit wird wie folgt definiert:

Das komplexe Zahlenformat, bei dem a eine reelle Zahl und b eine imaginäre Zahl ist, wird wie folgt definiert:

Im Gegensatz zum reellen Zahlensystem, in dem alle Zahlen auf einer Linie dargestellt werden, werden komplexe Zahlen auf einer komplexen Ebene dargestellt, wobei eine Achse reelle Zahlen und die andere Achse imaginäre Zahlen darstellt.




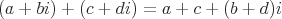



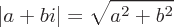


Ein Logarithmus ist eine Funktion, die für eine bestimmte Zahl die Potenz oder den Exponenten zurückgibt, die/der erforderlich ist, um eine gegebene Basis auf diese Zahl zu erhöhen. Einige Vorteile der Verwendung von Logarithmen sind sehr groß und sehr kleine Zahlen können durch kleinere Zahlen dargestellt werden. Ein weiterer Vorteil von Logarithmen ist, dass einfache Addition und Subtraktion gleichwertige, komplexere Operationen ersetzen. Die Definition eines Logarithmus lautet:
 ,
wobei
,
wobei  und
und 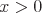
 , where
, where 





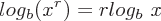
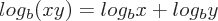

Ein Polynom ist ein Ausdruck, der aus Variablen und Konstanten besteht und die Operatoren Addition, Subtraktion, Multiplikation, Division und Potenzierung mit einer konstanten nicht negativen Zahl verwendet. Polynome haben die folgende Form:

Das Polynom besteht aus Koeffizienten multipliziert mit der Variable hoch einer ganzzahligen Potenz. Der Grad eines Polynoms wird durch die größte Potenz bestimmt, mit der die Variable potenziert wird.
Eine quadratische Gleichung ist ein Polynom zweiter Ordnung.

Die Lösung einer quadratischen Gleichung ist die quadratische Formel. Die quadratische Formel lautet:
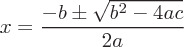
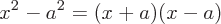

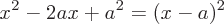
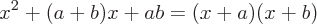




Die Quadratwurzel ist eine Funktion, bei der die Quadratwurzel einer Zahl (x) eine Zahl (r) ergibt, deren Quadrieren gleich x ist.
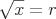 und
und 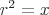
Auch die Quadratwurzeleigenschaft lautet:
wenn  dann
dann 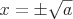
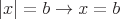 oder
oder 

 oder
oder 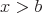
Quadrat vervollständigen ist eine Methode zum Lösen quadratischer Gleichungen. Algebraische Eigenschaften werden verwendet, um das quadratische Polynom zu manipulieren und seine Form zu ändern. Diese Methode ist eine Möglichkeit, die quadratische Formel abzuleiten.

Die Schritte zum Vervollständigen des Quadrats sind:
Ausdrücke, die an inkrementellen Punkten ausgewertet und dann in einem kartesischen Koordinatensystem dargestellt werden, ergeben ein Diagramm oder einen Graphen.
Wenn eine Funktion gleich einer Konstanten ist, ist f(x) für alle Werte von x gleich der Konstanten. Der Graph dieser Funktion ist eine Gerade durch den Punkt (0,c).

Eine lineare Funktion hat die Form:

Der Graph dieser Funktion hat eine Steigung von m und der y-Achsenabschnitt ist b. Er verläuft durch den Punkt (0,b). Die Steigung wird wie folgt definiert:
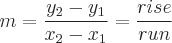
Eine Additionsform für lineare Funktionen ist die Punktsteigungsform:

Eine Parabel ist eine grafische Darstellung einer quadratischen Funktion.

Die Grafik einer Parabel in dieser Form öffnet sich nach oben, wenn a>0, und nach unten, wenn a<0. Der
Scheitelpunkt der Parabel befindet sich an:
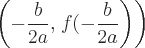
Andere Formen von Parabeln sind:
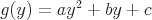
Der Graph einer Parabel in dieser Form öffnet sich nach rechts, wenn a>0, oder nach links, wenn a<0. Der Scheitelpunkt der Parabel befindet sich
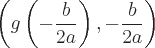
Die Funktion eines Kreises folgt der Form:

Wobei der Mittelpunkt des Kreises (h,k) und der Radius des Kreises r ist.
Die Funktion einer Ellipse folgt der Form:

Wobei der Mittelpunkt der Ellipse (h,k) ist
Die Funktion einer Hyperbel, die sich vom Mittelpunkt nach rechts und links öffnet, folgt der Form:
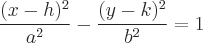
Die Funktion einer Hyperbel, die sich vom Mittelpunkt aus nach oben und unten öffnet, folgt der Form:
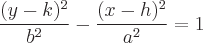
Wobei der Mittelpunkt der Hyperbel (h,k) ist, mit Asymptoten, die durch den Mittelpunkt verlaufen, mit Steigungen von:
