Czy wolisz polską wersję strony elektroda?
Nie, dziękuję Przekieruj mnie tam
Finden Sie die Definitionen der trigonometrischen Funktionen eines Winkels Theta, indem Sie einem der Winkel in einem rechtwinkligen Dreieck diesen Wert zuweisen. Die Sinus-, Kosinus- und Tangensfunktionen können mit den Eigenschaften eines rechtwinkligen Dreiecks definiert werden. Ein rechtwinkliges Dreieck hat einen Winkel mit einem Wert von 90 Grad. Die längste Seite des Dreiecks ist die Hypotenuse. Die Seite gegenüber von Theta wird als gegenüberliegend bezeichnet. Die zweite Seite neben Theta wird als angrenzend bezeichnet. Es gibt folgende Eigenschaften:
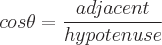
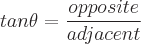
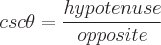
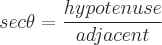
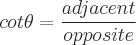
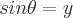
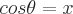
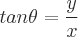
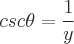
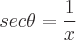
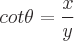
Mögliche Eingangswinkelwerte für jede Funktion sind unten definiert:
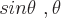kann ein beliebiger Winkel sein
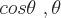kann ein beliebiger Winkel sein
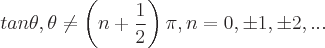
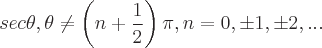
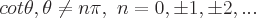
Bereiche der möglichen Werte für jede dieser Funktionen sind:
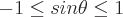
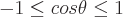
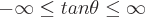
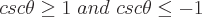
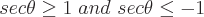
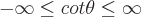
Perioden für jede dieser trigonometrischen Funktionen sind:
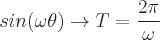
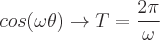
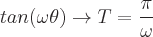
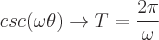
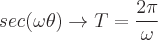
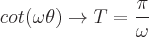
Definitionen der inversen trigonometrischen Funktionen sind:
Inverse trigonometrische Funktionen werden auch als bezeichnet:
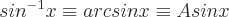
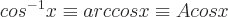
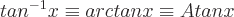
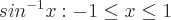
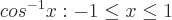
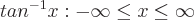
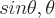kann ein beliebiger Winkel sein
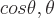kann ein beliebiger Winkel sein
