

Czy wolisz polską wersję strony elektroda?
Nie, dziękuję Przekieruj mnie tam
In der Trigonometrie ist das Sinusgesetz, auch als Sinusregel bekannt, sehr nützlich zum Lösen von Problemen mit Dreiecken, da es für jede Form eines Dreiecks funktioniert.
![]()
Das Kosinusgesetz, auch als Kosinusregel bekannt, ermöglicht es uns, die fehlenden Teile eines Dreiecks zu lösen, wenn zwei Seiten und der Winkel zwischen ihnen bekannt sind.
a2 = b2 + c2 – 2bc cosα
b2 = a2 + c2 – 2ac cosβ
c2 = a2 + b2 – 2ab cosγ
Beachten Sie, dass a, b und c alle drei Seiten des Dreiecks darstellen, während γ den bekannten Innenwinkel darstellt.
Das Tangensgesetz, auch als Tangensregel bekannt, definiert die Beziehung zwischen der Länge der gegenüberliegenden Seiten und den Tangenten zweier Innenwinkel eines Dreiecks.
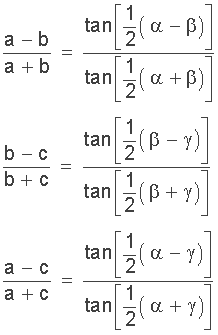
Für trigonometrische Gesetze ist Mollweides Formel eine Gleichung, die die Beziehung zwischen drei Seiten und den Winkeln eines Dreiecks definiert und zur Überprüfung der vorherigen trigonometrischen Gesetze eines Dreiecks verwendet werden kann.
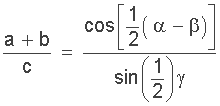
Identitäten für die Tangens- und Kotangensfunktionen können aus ähnlichen Formeln abgeleitet werden, die für die Sinus- und Kosinusfunktionen verwendet werden. Die Identität für Tangenten ist wie folgt:
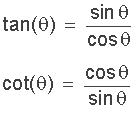
Die reziproken Identitäten Regel sind im Grunde Definitionen der Reziproken der drei vorherigen trigonometrischen Verhältnisse und als solche sind sie wichtige trigonometrische Identitäten, die wir verwenden können, um verschiedene trigonometrische Probleme zu lösen.
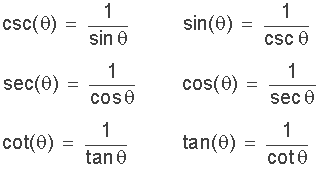
Wie der Name schon sagt, werden Pythagoreische Identitäten aus dem Standard-Pythagoras-Theorem für rechtwinklige Dreiecke abgeleitet.
sin2θ + cos2θ = 1
tan2θ + 1 = sec2θ
cot2θ + 1 = csc2θ
Trigonometrische gerade und ungerade, oder ungerade und gerade Identitäten zeigen, ob jede trigonometrische Funktion eine ungerade Funktion oder eine gerade Funktion ist.
sin(–θ) = –sin(θ)
cos(–θ) = cos(θ)
tan(–θ) = –tan(θ)
csc(–θ) = –csc(θ)
sec(–θ) = sec(θ)
cot(–θ) = –cot(θ)
Eine periodische Funktion ist eine Funktion, die sich ständig in regelmäßigen Abständen über die Zeit wiederholt, wie die Sinusfunktion. Wenn sie auf einem Graphen dargestellt wird, ist die Form einer periodischen Funktion symmetrisch und wiederholt sich entlang der horizontalen X-Achse. Sinusförmige Wellenformen sind periodische Funktionen.
sin(θ + 2πn) = sin(θ)
cos(θ + 2πn) = cos(θ)
tan(θ + πn) = tan(θ)
csc(θ + 2πn) = csc(θ)
sec(θ + 2πn) = sec(θ)
cot(θ + πn) = cot(θ)
Für die Kosinus-Doppelwinkel-Identität gibt es drei Formen der Identität, die wir aus der Grundform, cos(2α) = cos2(α) – sin2(α) unter Verwendung der Pythagoreischen Identität erstellen können.
sin(2θ) = 2sinθcosθ
cos(2θ) = cos2θ – sin2θ = 2cos2θ – 1 = 1 – 2sin2θ
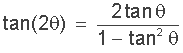
Wie der Name schon sagt, haben Halbwinkel-Identitäten oder Funktionen Halbwinkel in sich. Beachten Sie, dass das ±-Zeichen einfach bedeutet, dass das Ergebnis der Quadratwurzel positiv oder negativ sein kann, je nachdem, in welchem Quadranten der Winkel liegt.
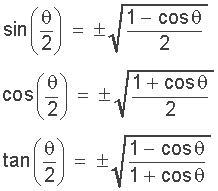
In der Trigonometrie werden die Summen- und Differenzen Identitäten verwendet, um den Wert einer trigonometrischen Funktion bei einem bestimmten Winkel in Bezug auf zwei Winkel zu finden, die bekannte trigonometrische Werte haben. Zum Beispiel 75o = 60o + 15o.
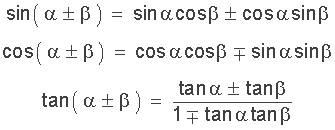
Ein Produkt-zu-Summe Identität kann verwendet werden, um das Produkt der Sinus- und Kosinusfunktionen als Summe darzustellen. Die Produkt-zu-Summe-Identität basiert auf den vorherigen Summen- und Differenzen-Identitäten, die in der Trigonometrie verwendet werden.
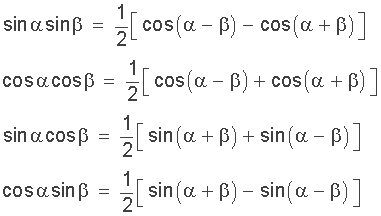
Die Summe-zu-Produkt Identität wird verwendet, um die Summe und Differenz von Sinus- und Kosinusfunktionen als Produkte ihrer Sinus- und Kosinusfunktionen auszudrücken. Das heißt, sie kann den Unterschied einer Sinusfunktion zum Unterschied einer Kosinusfunktion als die summierte Produkt dieser beiden Funktionen ausdrücken.
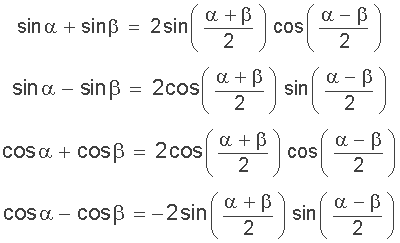
Kofunktions-Identitäten zeigen die Beziehung zwischen den verschiedenen komplementären Winkeln und den trigonometrischen Funktionen, die zwischen den Sinus- und Kosinus-, Tangens- und Kotangens- sowie Sekans- und Kosekanspaaren existieren. Wir können die Winkelsummen-Eigenschaft eines rechtwinkligen Dreiecks verwenden, um die sechs Kofunktions-Identitäten abzuleiten.
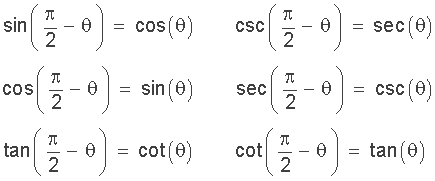
In diesem Trigonometrische Gesetze und Identitäten Tutorial haben wir gesehen, dass diese trigonometrischen Gesetze und Regeln sehr nützlich sind, um Dreiecke unter Verwendung der Werte, die sich auf ihre Seiten und Winkel beziehen, zu lösen.
Wir haben auch gesehen, dass es klare Beziehungen für Tangens, Kotangens, Sekans und Kosekansausdrücke in Bezug auf Sinus und Kosinus gibt, was diese Identitäten in realen Situationen nützlich macht. Beachten Sie, dass die pythagoreische Formel für die Gesetze der Sinus und Kosinus eines der wichtigsten trigonometrischen Gesetze und Identitäten ist, die in der Elektro- und Elektroniktechnik verwendet werden.