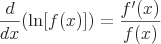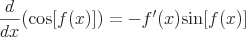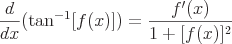Czy wolisz polską wersję strony elektroda?
Nie, dziękuję Przekieruj mnie tam
Grenzwertdefinition
Begrenzung für die rechte Hand
Limit für die linke Hand
Grenze bei unendlich
Eigenschaften begrenzen
Bewertung begrenzen. in +-Unendlich
Bewertungsmethoden einschränken
Kontinuierliche Funktionen
Kontinuierliche F&C.
Überlegen und abbrechen
L'Hospitals-Regel
Definition_of_a_Derivative">Definition eines Derivats
Mittelwertsatz
Grundlegende Eigenschaften
Produktregel
Quotientenregel
Machtregel
Kettenregel
Gemeinsame Derivate
Beispiele für Kettenregeln
Ein Grenzwert ist eine Methode zum Auswerten eines Ausdrucks, wenn sich das Argument seinem Wert nähert. Dieser Wert kann ein beliebiger Punkt auf der Zahlengeraden sein, und häufig werden Grenzwerte ausgewertet, wenn sich das Argument der Unendlichkeit oder minus Unendlich nähert. Der folgende Ausdruck besagt, dass sich die Funktion dem Wert von L annähert, wenn sich x dem Wert von c nähert.

Der folgende Ausdruck besagt, dass sich x dem Wert von c nähert und x > c nähert sich die Funktion dem Wert von L.

Der folgende Ausdruck besagt, dass x sich dem Wert von c nähert und x < c nähert sich die Funktion dem Wert von L.
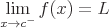
Der folgende Ausdruck besagt, dass der Wert von c eine sehr große und positive Zahl ist und sich die Funktion dem Wert von L nähert, wenn sich x der Unendlichkeit nähert.
 < /p>
< /p>
Auch der Grenzwert, wenn x sich der negativen Unendlichkeit nähert und der Wert von c eine sehr große und negative Zahl ist, wird unten ausgedrückt.
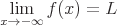
Unter Berücksichtigung der folgenden Bedingungen:

Die folgenden Eigenschaften sind vorhanden:
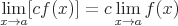


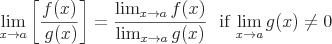
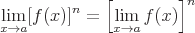





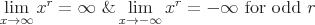
Wenn f(x) an a kontinuierlich ist, dann:
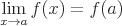
Wenn f(x) an a kontinuierlich ist, dann b:


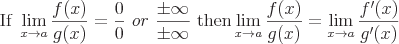
Die Ableitung ist eine Möglichkeit, zu definieren, wie sich die Ausgabe eines Ausdrucks ändert, wenn sich die Eingaben ändern. Unter Verwendung von Grenzwerten wird die Ableitung wie folgt definiert:

Dies ist eine Methode zur Annäherung an die Ableitung. Die Funktion muss über das Intervall (a,b) differenzierbar sein und a < c < b.

Wenn es eine Ableitung für f(x) und g(x) gibt und c und n reelle Zahlen sind, gilt Folgendes:

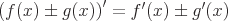

Die Produktregel gilt, wenn differenzierbare Funktionen multipliziert werden.
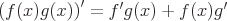
Die Quotientenregel gilt, wenn differenzierbare Funktionen geteilt werden.

Die Potenzregel gilt, wenn eine differenzierbare Funktion potenziert wird.

Zasada łańcucha ma zastosowanie, gdy funkcja różniczkowalna jest stosowana do innej funkcji różniczkowalnej.


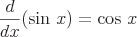




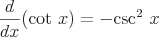

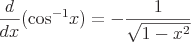

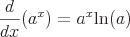

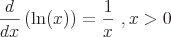
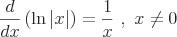

Oto kilka przykładów typowych instrumentów pochodnych, które wymagają reguły łańcuchowej.